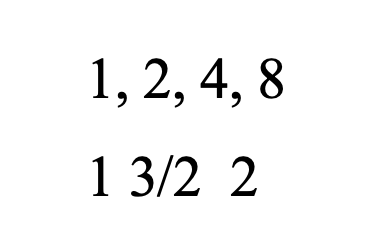*Álvaro Carvajal Villaplana
Platón: materia y geometría
Parte VI
La entrega para la columna Nuevas Perspectivas correspondiente a la noción de materia en Platón se dividió en dos partes: la primera (Parte V), se abordó los temas de la contribución de Platón a la filosofía de la ciencia, el estatus epistemológico de su teoría de la materia y la materia como realidad indeterminada. Esta segunda sección (Parte VI), comprende los temas de los 4 elementos y su estructura geométrica, la construcción de los sólidos, y la estructura del alma del mundo.
Los cuatro elementos y su estructura geométrica
Para Platón los cuatro elementos no eran en realidad elementos últimos constitutivos de la materia, irreductibles a otros e intransformables, como en el caso de Empédocles, para quien los cuatro elementos son el último estadio real para entender lo orgánico. Para él, son un dato sensible. Platón en cambio los concibe como un dato teórico, es decir, no se deducen por intuición, sino que hay razones apriorísticas para afirmarlas (Coronado, en Carvajal 1989).
Para Platón la naturaleza está llena de números (al igual que los pitagóricos), que son los verdaderos entes metafísicos intermediarios entre las formas puras y las “cosas”, que operan también como causas segundas. Los cuatro elementos se vuelven a introducir bajo apariencias geometrizantes, en orden creciente de complejidad. De tal manera que la explicación de la materia y de sus propiedades se ofrece en términos de figuras geométricas, lo que está conforme -en gran medida- con la tradición pitagórica (Losse, 1973/1981, 29).
Los 4 elementos son cuerpos, por cuanto tienen espesor, superficies y triángulos; es decir, son poliedros regulares. A cada elemento le corresponde un poliedro regular (Coronado en sus clases enfatizó en esta explicación, incluso llevó las figuras tridimensionales al aula para experimentáramos con ellas). Autores como los citados a continuación sugieren que Platón vislumbra en el Timeo que los 5 elementos (4 terrestres y un celeste) pueden ser correlacionados con los 5 sólidos regulares (Losse, 1972/1981, 29); por su parte, Wartosfky asevera que los 5 poliedros regulares conversos, son a la vez, los elementos básicos, de lo que Platón denominó cosmos (1968/1983, 120). Así se tiene que Platón asignó el tetraedro al fuego, porque el tetraedro es el sólido regular con los ángulos agudos más agudos; además, debido a que el fuego es el más penetrante de los elementos. Adjudicó el cubo a la tierra, porque al voltear un cubo sobre una base cuesta más esfuerzo que voltear otro de los tres sólidos restantes, y porque la tierra es el más sólida. Al aire al octaedro, por cuanto su tamaño, peso y fluidez ocupa un punto intermedio, y al agua al icosaedro, por ser el más móvil y fluido de los elementos.
Si se asume la sugerencia anterior, de una materia celeste, dicho quinto elemento, sería representado por el dodecaedro, por ser la figura que más se acerca a la esfera, y debido a que el éter es un elemento especial. Estas figuras son del grupo de las figuras cerradas con líneas rectas, la figura de línea curva por excelencia es la esfera que corresponde al cuerpo del cosmos.
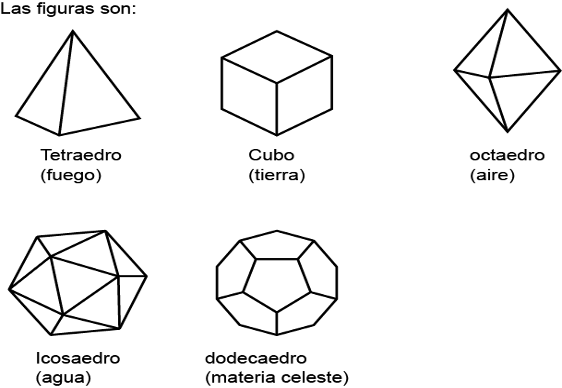
(Losse, 1972/1981, 29).
El triángulo es la figura plana “más sencilla” y el elemento básico de la concepción platónica del cosmos y la materia, ya que son irreductibles, así como principio de todos los otros. El privilegio de los poliedros consiste en contener superficies formadas por triángulos que son iguales, con líneas, y puntos de simetría, por ejemplo,

(ver Wartosfky, 1868/1983, 120).
Para Platón, las figuras antecedentes permiten la transmutabilidad, de tal manera que sugirió que las transformaciones entre agua, aire y fuego provienen de la disolución de cada triángulo equilátero a los sólidos regulares respectivos en 6 triángulos de 30º, 60º y 90º, con la subsecuente recombinación de tales triángulos más pequeños para formar caras de otros sólidos regulares (Losse, 1972/1981, 29). El único poliedro que no es transmutable es el cubo. Por otra parte, los elementos no se transforman los unos en los otros, sino que el cambio se da a partir de los triángulos más pequeños que pueden descomponerse, como se expondrá.
Se postulan dos triángulos básicos: (1) el triángulo rectángulo isósceles y (2) el triángulo rectángulo escaleno. El triángulo isósceles solo puede tener una forma, son semejantes entre sí. El triángulo escaleno puede tener muchas formas, por el cambio de proporciones de sus lados. El triángulo escaleno al repetirse dos veces o al añadirse a sí mismo, forma un tercer triángulo, el equilátero. Tenemos que tres de los poliedros regulares nacen de triángulos escalenos y uno (el cubo) de triángulos isósceles; por tanto, solo tres de ellos pueden transformarse los unos en los otros. La transformación se produce a partir de la subsecuente combinación de estos triángulos (escalenos), es decir, que al ser dividirlos pueden volverse a recomponer en otro orden y dar razón de la transmutabilidad mutua de dichos elementos. El cubo no puede transformarse en otros, ya que los triángulos isósceles solamente pueden recomponerse en nuevas superficies cuadradas, y ella a la vez en cubos. Por lo que se tiene las siguientes combinaciones:
| Elemento | Representación | No. de caras | Triángulo | Básico |
| Tierra | Cubo | 6 | Isósceles | 24 |
| Fuego | Tetraedro | 4* | Escalenos | 24 |
| Aire | Octaedro | 8* | Escalenos | 48 |
| Agua | Icosaedro | 20* | Escalenos | 120 |
* Cada “cara” requiere de 6 triángulos básicos.
Fuetne: Coronado, en Carvajal, 1989.
Construcción de los sólidos (dos ejemplos)
Para la construcción del tetraedro se necesitan seis triángulos escalenos para formar una superficie. Los catetos se unen siguiendo la diagonal. Esto se realiza tres veces:
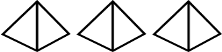
Luego, las diagonales y los catetos deben concurrir en un mismo punto o punto de simetría (Losse, 1972/1981, 29):

Esto se repite cuatro veces, y por la unión de tres triángulos planos se forma un ángulo más obtuso:
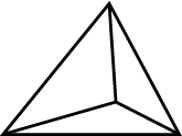
El octaedro se compone de ocho triángulos equiláteros formando un sólido de cuatro ángulos planos, siguiendo el método anterior.
Estructura: matemática del alma del mundo
La estructura matemática del alma del mundo que da sentido a los cuerpos y se impone a estos, se da por un proceso en el que se encuentran en dos momentos: (1) cuando se establece la necesidad de los cuatro elementos y (2) cuando los términos medios que no están agrupados, sino, intercalados.
La clase de estructura del mundo tiene que ver con las proporciones, que son ciertas relaciones que se establecen entre tres términos, dos externos y un medio. Se puede hablar del medio geométrico; dado los números se pueden encontrar en una relación particular en medio. Las relaciones son: aritmética, geométrica, armónica y armónica continua, así que

(Robin, 1957, 59)
Se plantea la serie total: 1, 2, 3, 4, 8, 9, 27, a partir de esta división se da la separación en intervalos.
Aritmética: el primer número excede al segundo por la misma cantidad en que el segundo excede al tercero.
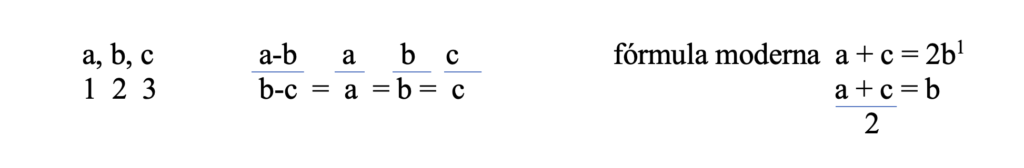
Una de las formas de definir los intervalos es el media aritmética (utilizando la fórmula):
Medio geométrico: en el primero es al segundo como el segundo al tercero
a : b Fórmula moderna ac = b2
b c por ejemplo, 2 4 8. La razón del duplo.
No se usa esta, para crear las series, sino, solo la armonía y la aritmética.
Medio armónico: dos números, el primero excede al segundo, el segundo excede al tercero por la misma cantidad.

Por eso hay cuatro elementos, se justifica el dato de los cuatro elementos de Empédocles (a priori). Cada elemento tiene una estructura matemática.
La teoría es satisfactoria porque llena los requisitos planteados por los jónicos: (a) la razón, sentido de regularidad, sistematicidad y simplicidad. (b) los sentidos, explica el mundo de lo cambiante a partir de los cuatro elementos de modo geometrizante y matemático.
La dificultad de la teoría consiste en preguntarse si la realidad última de las cosas existe, es decir, cómo es que existe o qué es lo que sustenta la existencia de las ideas. Esta es la misma crítica que le hace Platón a los atomistas.
Bibliografía
Arana, Juan. (2001) Materia, universo, vida. Madrid: Tecnos.
Casini, Paolo. (1975/1977). Naturaleza. Barcelona: Labor.
Cornford, F.M. (1967/1974). La filosofía no escrita. Barcelona: Ariel.
Carvajal Vilaplana, Álvaro. (1989) Historia de la noción de materia. Apuntes de clase del Curso de Guillermo Coronado, F-2024 Filosofía de la Naturaleza. San José, C.R.: Escuela de Filosofía, Universidad de Costa Rica. Inédito.
Junceda, José Antonio. (1975). De la mística del número al rigor de la idea. Sobre la prehistoria del saber occidental.Madrid: Fragua.
Farrington, Benjamin. (1969/1980). Ciencia y filosofía en la antigüedad. 6ta. Ed, Barcelona: Ariel
Ferrater Mora, José (1994/199). Diccionario de filosofía. Tomo III. Barcelona: Ariel.
Hiller, Horst. (1968). Espacio-Tiempo. Materia-infinito. Madrid: Gredos.
Lange, F.A. (1974). Historia del materialismo. Tomo I. México: Juan Pablos Editor.
Losse, John. (1972/1981). Introducción histórica a la filosofía de la ciencia. 3ra. Ed. Madrid: Alianza.
Robin, León. (1957). El pensamiento griego y los orígenes del espíritu científico. México: Unión Tipográfica Editorial Hispano Americana.
Wartofsky, Marx. (1968/1983). Introducción a la filosofía de la ciencia. 2da. Ed. Madrid: Alianza.
[1] Las fórmulas corresponden a mis apuntes de clases.